Enhancing HAVOK: Truncation Bounds, Data Reduction, and Rare Event Prediction

Download

• Paper

Abstract

Data-driven techniques have become indispensable for analyzing nonlinear and chaotic dynamical systems, where traditional models fall short. In this work, we build upon the HAVOK (Hankel Alternative View of Koopman) framework to improve the analysis and prediction of such systems. We derive an upper bound on the truncation rank in HAVOK analysis by leveraging the exponential decay structure of singular values in chaotic systems, filling a gap in the literature where no robust systematic approach to rank selection previously existed. Additionally, we introduce a method to significantly reduce the amount of measurement data required for accurate HAVOK reconstruction, addressing the practical bottleneck of HAVOK’s relatively high computational cost and the absence of existing acceleration techniques. Finally, we test the power of singular vectors to predict rare events in chaotic systems, such as lobe switching in the Lorenz attractor, exploiting increases in activity of SVD coordinates as a sign of an impending event. Together, these contributions pave the way for future promising research on data-driven methods in the study of chaotic dynamics.

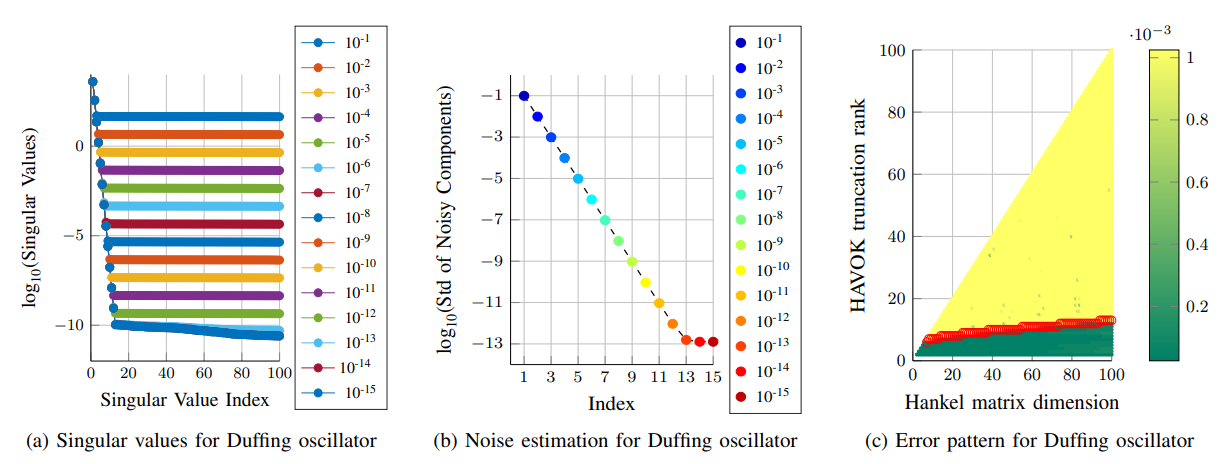
Figure 6: Summary of results for Duffing oscillator

Citation

Snytko V. 2025. “Enhancing HAVOK: Truncation Bounds, Data Reduction, and Rare Event Prediction.” https://vladsnytko.com/papers/enhancing-havok/Enhancing_HAVOK.pdf.

@article{snytko2025havok,
author = {Vladislav Snytko},
year = {2025},
title ={Enhancing HAVOK: Truncation Bounds, Data Reduction, and Rare Event Prediction},
url = {https://vladsnytko.com/hugo-website/papers/enhancing-havok/Enhancing_HAVOK.pdf}}